Basic 2d Fluidsolver in vex

The last few weeks, I’ve been playing around with an SPH fluid solver that I’ve implemented in VEX. It’s been a lot of fun, and I wanted to share and explain the setup, because implementing it was easier than expected.

What is SPH? SPH is a method to simulate fluids and gases. If you’re familiar with FLIP or Vellum Fluid in Houdini, you’ll find some similarities here - they’re all particle-based systems. The basic idea is to represent a fluid as a collection of particles that interact with each other. SPH works by calculating Pressure and viscosity based on the density of the points.

Initially, I intended for this to be a guide on how to set up the system, but I later decided against it. Instead download the file here and read along with the rest of this blog, or just start playing around.

If you want to support this little exploration and get your hands on the project file for the video above you can buy it on gumroad.

Be aware, I’m not an expert in this field, there might be some things wrong with this implementation or my explanations aren’t 100% on point.

Quick Walkthrough

First off, let’s quickly run through the whole simplified SPH workflow, which looks like this:

Particle Setup: We start by creating our particles and assigning them initial properties such as position, velocity, and mass.

Main Simulation Loop, for each frame of our simulation, we’ll run through these steps:

1. Neighbor Search: Find neighboring points.

2. Density Calculation: Determine how “crowded” each area of our fluid is by looking at how many particles are nearby.

3. Force Calculations: Compute various forces acting on each particle using Kernel functions:

   • Pressure Force: Particles pushing each other.
   • Viscosity Force: Fluid resistance.
   • External Forces: Such as gravity.

4. Integration: Update the particles using the calculated forces.

5. Boundary Handling: Ensure our particles don’t escape the simulation area or pass through solid objects.

Implementation

We’ll start by creating some points. Next up we will set up mass, and velocity attributes. The default value for mass is 1.0 and represents water.

f@mass = 1.0;
v@v   = curlnoise(@P/4)*82;
v@v.y = 0;  // Set to 0 for 2d noise

1. Neighbor search

Inside the solver we start by loading the point neighbors of each particle into an array. The dist variable controls the search radius for each point. neighborCount, as you might have guessed, controls the number of neighbors each particle has. In SPH simulations, a typical neighborCount ranges from 20 to 100 neighbors per particle.

float dist = chf("dist"); // set to 1.0
int neighbourCount = chi("neighborCount");
int neighbors[] = pcfind(0, "P", @P, dist, neighbourCount); // can also use nearpoints()

Simulation Parameters

These following attributes set the behavior of our fluid, which in this “default” state would be water. You can find a list of all these attributes and what they do here

// SPH parameters
// controlling the range of particle interactions
float viscosityCoefficient = 1.0; // Controls the viscosity of the fluid
float restDensity = 1000.0; // Specifies the rest density of the fluid, typically 1000 for water
float k = 1000.0; // Stiffness constant
float deltaTime = 0.002; // Time step for the simulation

2. Kernel Functions

The “Smoothed” part of Smoothed Particle Hydrodynamics comes from functions known as “smoothing kernels.” These are specifically designed to approximate fluid behaviors and properties. In our case they are used to model density, pressure, and viscosity. Kernel functions calculate the amount of influence a particle has on its neighbors based on their distance.
The max range h range is controlled through our smoothingLength. The influence typically decreases as the distance increases, ensuring that particles farther away have less impact. Since our max distance to neighboring Points has been set with our dist attribute our smoothingLength should be the same, or lower than dist.

float smoothingLength = chf("smoothingLength");

// Poly6 Kernel
float kernel(float q; float h) {
    if (q >= 0 && q <= h) {
        return (315.0 / (64.0 * PI * pow(h, 9))) * pow(h * h - q * q, 3);
    } else {
        return 0.0;
    }
}

// Spiky Kernel
vector gradientKernel(vector r; float h) {
    float q = length(r);
    if(q == 0) return set(0, 0, 0);
    return -45.0 / (PI * pow(h, 6)) * (r / q) * pow(h - q, 2);
}

// Viscosity Kernel
float velocityKernel(float q; float h) {
    if (q >= 0 && q <= h) {
        return (45.0 / (PI * pow(h, 6))) * (h - q);
    } else {
        return 0.0;
    }
}

Density Calculation

The core of Smoothed Particle Hydrodynamics is the density calculation, it is calculated by summing up the contributions from nearby particles, smoothing them with one of the aforementioned kernel Functions.

// Density Estimation
float density = 0.0;
foreach (int neigh; neighbors) {
    vector r = @P - point(0, "P", neigh);
    float q = length(r);
    density += point(0, "mass", neigh) * kernel(q, smoothingLength);
}

// Update density attribute for the current particle
@density = density;

Pressure

The next step is calculating the pressure based on the difference between the current density and the restDensity, scaled by the stiffness constant k, and ensure the pressure isn’t negative.¹

The restDensity represents the target or equilibrium density of the fluid. It is the density that the fluid would ideally maintain if it were in a state of rest and equilibrium. Whereas the stiffness constant k determines how much the fluid resists compression and thus affects how quickly pressure builds up when the fluid is compressed.

// Pressure Calculation
@pressure = max(0.0, k * (@density - restDensity)); //non negative pressure

Pressure & Viscosity Force

Once the pressure is calculated, the next step is to compute the pressure force between particles.

Pressure force is a vector that pushes particles away from high-density areas and pulls them towards low-density areas. This force is calculated using the gradientKernel() function for each neighbor.

Viscosity forces simulate the internal friction of the fluid, making it either sticky or smooth, using the velocityKernel(). The force helps to distribute momentum between particles. The classic example would be honey versus water: honey, with high viscosity, pulls more on particles, making it thicker and more cohesive, while water, with low viscosity, allows particles to separate more easily.

// Force Calculation
vector totalPressureForce = {0, 0, 0};
vector totalViscosityForce = {0, 0, 0};
foreach (int neigh; neighbors) {
	vector r = @P - point(0, "P", neigh);
	float q = length(r);
	
	// Pressure force
	float neighborPressure = point(0, "pressure", neigh);
	float neighborDensity = point(0, "density", neigh);
	
	totalPressureForce += -float(point(0, "mass", neigh)) * 
		((@pressure / (neighborDensity * neighborDensity)) + 
		(neighborPressure / (neighborDensity * neighborDensity))) 
		* gradientKernel(r, smoothingLength);
	
	// Viscosity force
	vector neighborVelocity = point(0, "v", neigh);
	totalViscosityForce += viscosityCoefficient * float(point(0, "mass", neigh)) 
		* (neighborVelocity - @v) / neighborDensity * velocityKernel(q, smoothingLength);
}

Integration

The last step is to apply all the calculated forces, which is done through “integration methods.” There are a bunch of different integration methods, each with strengths and weaknesses,² but in essence all of these methods do the same thing, convert the previously calculated forces into point velocities.

We are going to be using the “velocity Verlet” integration method, which is a good balance between accuracy and efficiency. This method requires an acceleration vector, which is calculated using the pressure and viscosity forces. This is also the place to add external forces like gravity.

vector gravity = {0,0,0}; // set gravity

// Integration Step (velocity Verlet  Integration)
// Calculate acceleration
vector acceleration = (totalPressureForce + totalViscosityForce) / @mass + gravity;

// Update position
@P += @v * deltaTime + 0.5 * acceleration * deltaTime * deltaTime;

// Update velocity
@v += acceleration * deltaTime;

Boundary

To get proper boundary interactions, we need to reflect the velocity using the dot product to ensure particles bounce off the boundary rather than pass through it. Additionally, we re-position particles just inside the boundary to prevent them from sticking at the edge and apply a dampening factor to simulate energy loss on impact.

vector center = {0, 0, 0};
float radius = 5.0;
float dampening = 0.95; // default should be 0.75

vector toCenter = @P - center;
float distance = length(toCenter);

if (distance > radius) {
    vector normal = normalize(toCenter);
    // Reflect Velocity
    @v -= 2 * dot(@v, normal) * normal * dampening;

    // set the points back into the circle with a little bit of offset, to break up edges
    @P = center + normalize(toCenter) * radius * (1.0 - abs(random(@ptnum) * 0.01));
}

Color

If we remap the density and map it to color, we get a cool representation of the underlying density.

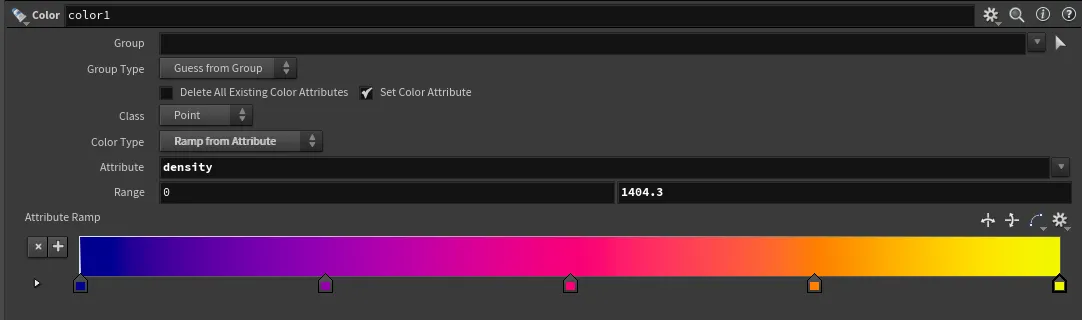
Done!

That’s it! Have fun playing around with it—set attributes per point, visualize different forces, or try it in 3D! I’ve included some examples in the project files, along with an implementation that includes drag.

If you want to support this small exploration, you can grab the scene files for the video at the start here. In there, you can see how I’ve combined SPH fluids with a particle life simulation to create these microbes swimming in water.

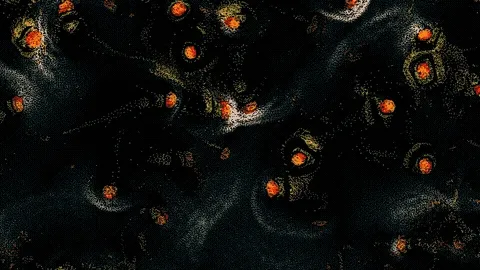
There is a lot that can be done in the future, like adding surface tension or implementing different fluid types, such as oil and water. If you create anything with this system, feel free to send it to me, I’d love to take a look at it :)

Thanks for reading - Jakob

Attributes

Smoothing Length

You need to play around with this alot! Start with half of the simulation search length and adjust from there to balance detail and stability. The radius within which particles influence each other. Larger smoothing lengths result in smoother interactions but can reduce simulation detail. Smaller smoothing lengths increase detail but may will lead to instability.

neighborCount

Should be between 20 - 100, using fewer neighbors can make the simulation faster but might reduce stability. This part of the system takes the most time to calculate, to improve performance consider lowering it.

DeltaTime

You can think of DeltaTime like substeps; a smaller delta time will improve the stability of the simulation because it calculates smaller steps. However, this will also make the simulation run slower. Start with a larger value like “0.001” and decrease it if instability occurs. Increase substeps on the SOP-Solver to offset slower simulations.

Rest Density

The target density for the fluid, influences the pressure calculation and overall stability. A higher rest density means particles will exert more pressure to reach this density. Tweaking Tips: Set based on the physical density of fluids. Common values for water are around 1000 kg/m³.

I think you can simulate oil and water if you set this in groups but haven’t tested that enough

viscosityCoefficient

Determines the fluid’s resistance to shear and flow. Higher values increase the damping and smooth out velocity differences between particles. Adjust based on the desired fluid behavior (e.g., honey vs. water). Higher values for more viscous fluids.

Gas Constant k

The stiffness constant k is used in the calculation of pressure. It determines how much the fluid resists compression and thus affects how quickly pressure builds up when the fluid is compressed.

Point Count

I like to keep it between 50.000 and 500.000 for quick results. If you scale up the point Count you might want to increase the size of the bounds as well as search distance and smoothing length.

Sources and Links

Particle-Based Fluid Simulation for Interactive Applications - 2003 - Matthias Müller, David Charypar and Markus Gross

The SPH equations - Bindel, Fall 2011 (some pseudocode instead of equations)

AMD - Video Smoothed Particle Hydrodynamics

Footnotes